![]()
Confidence
Interval for Proportions:
A Bayesian Approach
Home | Academic Articles
Purpose
The purpose of constructing a confidence
interval for proportions using a Bayesian approach is reduce the margin of
error from the Frequentist school confidence interval for proportions.
Example
To illustrate, suppose a store stocks boxes of
Brand X cereal each day so that there are 100 boxes in total. On day 1, they
sell 62 boxes. What is the 95% confidence interval of the percentage of boxes
sold per day?
Using the Frequentist school approach, the
interval would be:
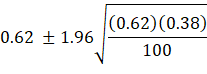
![]()
![]()
The width of the interval is 0.7151 – 0.5249 =
0.1902. Nice and simple.
Now, to use the Bayesian approach, we need a
prior distribution for θ. Since we don’t have any prior distribution, we
can use the uniform distribution in which P(θ) = 1.
However, the uniform distribution is a special
case of the Beta distribution in which α = 1 and β = 1. As is well
documented in the literature, the Beta distribution is the conjugate prior of
the binomial distribution.
To find the posterior distribution for θ,
we combine the posterior distribution with the current data in which n
represents the total number of cases and x represents the number of successes.
When we do this, the posterior distribution of θ follows a Beta
distribution with α = x + α and β = n + β – x.
In our example, α = 62 + 1 = 63 and
β = 100 + 1 – 62 = 39. Note that the sum of α and β is 102. This
is due to the sum of n = 100, the prior α = 1 and the prior β = 1.
To construct the 95% confidence interval using
the Beta distribution, we need the 2.5th and 97.5th
percentiles of the Beta distribution with α = 63 and β = 39. For this
distribution, the 2.5th percentile is 0.5218 and the 97.5th
percentile is 0.7091. Thus, the interval is:
![]()
The width of this interval is 0.7091 – 0.5218
= 0.1873 which is a tad tighter than the 0.1902 from the previous confidence
interval.
Suppose that over the next 4 days, as on the
first day, there are 100 boxes on the shelf and these are the number of boxes
sold:
|
Day 2 |
Day 3 |
Day 4 |
Day 5 |
|
28 |
8 |
42 |
65 |
If we sum the number of sales over the 5 days,
p = 205/500 = 0.41. Then the 95% confidence interval from the frequentist
school is:
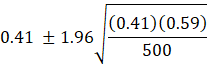
![]()
![]()
The width of this interval is 0.4531 – 0.3669
= 0.0862.
Using the Beta distribution, we find the new
values of α and β:
|
|
Prior |
Day 2 |
Day 3 |
Day 4 |
Day 5 |
Total |
|
α |
63 |
28 |
8 |
42 |
65 |
206 |
|
β |
39 |
72 |
92 |
58 |
35 |
296 |
Note that we use α = 63 and β = 39 as
the new priors. This time, the 2.5th percentile is 0.3677 and the
97.5th percentile is 0.4537. The width of this interval is 0.4537 –
0.3677 = 0.086. The width is still slightly less than that of 0.0862 but the
difference is narrowing. However, as explained in the technical details
section, the Bayesian confidence interval will always be narrower than the
frequentist school confidence interval, provided the total number of cases is
greater than 3.
Technical details
The formula for the Beta distribution is:
![]()
In the formula, ![]() represents the gamma function of α. The
formula for the gamma function is:
represents the gamma function of α. The
formula for the gamma function is:
![]()
If α is a whole number, then ![]() is
equal to (α – 1)!. For example, if α = 3, then
is
equal to (α – 1)!. For example, if α = 3, then ![]() = 2! =
2 x 1 = 2. It should be noted that in Excel, the factorial function is called
fact. So, in an Excel spreadsheet, to call 2!, you would type in a cell
=fact(2) to get the result of 2.
= 2! =
2 x 1 = 2. It should be noted that in Excel, the factorial function is called
fact. So, in an Excel spreadsheet, to call 2!, you would type in a cell
=fact(2) to get the result of 2.
For example,1 with α = 1 and β = 1,
we have:
![]()
![]()
![]()
This is due to the fact that 0! = 1 by
definition.
To eventually construct the posterior
distribution of θ, we can say:
![]()
The formula for the binomial distribution is:
![]()
In the formula, nCx is the number of ways to
choose x items from n. Its formula is:
![]()
In order to construct the posterior
distribution of θ, we can say:
![]()
In stats speak, f(x | θ) is called the
likelihood.
To construct the posterior distribution of
θ, we combine the prior and likelihood:
![]()
If there are a small number of cases or
successes, the Frequentist school has a tool at its disposal: Wilson’s
estimate. In using this tool, the sample proportion used in the interval is:
![]()
This raises the question as to why Bayesian
analysis is better when there are a small number of successes.
Let’s start with the mean and variance of the
Beta distribution.
![]()
![]()
In the case of the posterior distribution of
θ in which α = x + α and β = n + β – x, the mean and
variance are:
![]()
![]()
![]()
Let’s examine the case in which the prior is
the uniform distribution in which α = 1 and β = 1. The mean and
variance become:
![]()
![]()
If we take x equal to zero, the mean and
variance become:
![]()
![]()
If we examine the variance of θ using
Wilson’s estimate, we have:
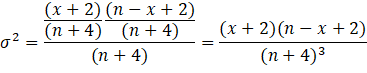
If we take x equal to zero, we have:
![]()
As is well documented, the variance (or
standard deviation) has an effect on the width of a confidence interval: A
larger variance results in a wider confidence interval.
This raises the question: For which values of
n is the variance of the Beta distribution less than that using Wilson’s
estimate?
![]()
![]()
![]()
The above inequality holds once n > 2. If x
is increased to 1, then the variance of the Beta distribution is less once n
> 3.