P-values – a Bayesian Perspective

---

Home | Academic Articles

---

Consider the following null and alternative hypotheses:

Ho: μ < 100

Ha: μ > 100

Suppose that σ = 25 and from a sample of 60, the sample mean = 106. We can calculate the Z value:

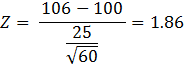
Since this is a right-tail Z test, the p-value = P(Z > 1.86) = 0.0314 = 3.14%. If we were testing at a 5% level of significance, we would reject the null hypothesis since the p-value is less than 5%.

The central limit theorem states that the p-value = P( > 106) given μ = 100, σ = 25 and n = 60. The integral would be:

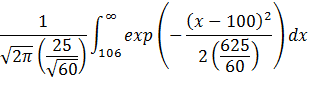
In the formula, we substitute x for .

If we let:

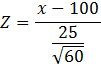
Then:

Substituting, we get:

This is simply P(Z > 1.86).

The above argument is from the frequentist school of thought: If we assume μ = 100, the p-value is the probability of obtaining a sample mean as great as 106 given σ = 25 and n = 60.

However, from the Bayesian school of thought, μ is a random variable with its own mean and standard deviation. At the same time, we have a sample mean of 106. This raises the question: Given = 106, σ = 25 and n = 60, what is P(μ < 100)?

The integral would be:

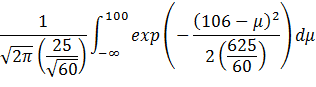
If we let:

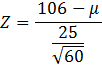
Then:

Substituting, we get:

The result is the same as the first integral.

Thus, from a Bayesian point of view, the p-value is the probability of the null hypothesis being true, given the data.