Seemingly Unrelated Regression
Model using Gibbs Sampler
Home | Academic Articles
Purpose
The purpose of the seemingly
unrelated regression (SUR) model using Gibbs sampler is to create a model that
has a better fit than the corresponding model under the Frequentist school.
Example
Let’s suppose we
have 3 sets of data to create 3 models.
Here is the first
data set:
|
y |
2.1 |
4.5 |
6.8 |
9.4 |
10.8 |
|
X1 |
1 |
2 |
3 |
4 |
5 |
And the second:
|
y |
4.8 |
9.6 |
13.7 |
19.6 |
21.4 |
|
X2 |
1 |
2 |
3 |
4 |
5 |
|
X3 |
0.25 |
0.42 |
0.84 |
1.32 |
1.64 |
And the third:
|
y |
0.5 |
1.1 |
1.4 |
2.3 |
3.4 |
|
X4 |
10.2 |
20.5 |
30.4 |
41.6 |
50.2 |
Using least squares, the summary statistics
for each of the coefficients are:
Model #1
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
Intercept |
0.03 |
0.3728 |
0.0805 |
0.9409 |
-1.1564 |
1.2164 |
|
X1 |
2.23 |
0.1124 |
19.8402 |
0.0003 |
1.8723 |
2.5877 |
Model #2
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
Intercept |
1.1418 |
2.1708 |
0.5260 |
0.6514 |
-8.1986 |
10.4822 |
|
X2 |
3.8261 |
2.9894 |
1.2799 |
0.3290 |
-9.0363 |
16.6886 |
|
X3 |
1.3420 |
8.0463 |
0.1668 |
0.8829 |
-33.2786 |
35.9626 |
Model #3
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
Intercept |
-0.3674 |
0.3177 |
-1.1562 |
0.3313 |
-1.3786 |
0.6438 |
|
X4 |
0.0689 |
0.0094 |
7.3223 |
0.0053 |
0.0390 |
0.0989 |
If all the variables are combined into one
model, this is the result:
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
Intercept |
0.0492 |
0.4615 |
0.1066 |
0.9172 |
-0.9791 |
1.0775 |
|
x1 |
2.2248 |
0.1557 |
14.2931 |
0.0000 |
1.8779 |
2.5716 |
|
x2 |
5.1036 |
0.9861 |
5.1753 |
0.0004 |
2.9064 |
7.3009 |
|
x3 |
-1.8103 |
2.9568 |
-0.6122 |
0.5540 |
-8.3984 |
4.7778 |
|
x4 |
0.0577 |
0.0153 |
3.7725 |
0.0036 |
0.0236 |
0.0918 |
The goal is to create models that solve for the
coefficients simultaneously. Arnold Zellner introduced a concept called the
seemingly unrelated regression (SUR) model.
As explained in the technical details, the
Gibbs sampler was run for 50,000 iterations.
If one has two models, the one that has the
lower sum of squared errors is the model with the better fit.
In regard to the sum of the squared errors, these are the results:
|
SUR |
Model
#1 |
Model
#2 |
Model
#3 |
Frequentist |
|
4.0339 |
0.379 |
3.3770 |
0.2719 |
4.6119 |
The sum of squared errors
is less for each of the individual models than for the SUR model which, in
turn, is less than that of the Frequentist model. It should be noted that when
the Gibbs sampler is run for 100,000 iterations, the sum of squared errors goes
down to 4.0331 which would seem to suggest that running the extra 50,000
iterations is not worth the while.
Technical details
In the SUR model, this is how the data would
be set up:
|
y1 |
x1 |
x2 |
x3 |
x4 |
|
2.1 |
1 |
0 |
0 |
0 |
|
4.5 |
2 |
0 |
0 |
0 |
|
6.8 |
3 |
0 |
0 |
0 |
|
9.4 |
4 |
0 |
0 |
0 |
|
10.8 |
5 |
0 |
0 |
0 |
|
4.8 |
0 |
1 |
0.25 |
0 |
|
9.6 |
0 |
2 |
0.42 |
0 |
|
13.7 |
0 |
3 |
0.84 |
0 |
|
19.6 |
0 |
4 |
1.32 |
0 |
|
21.4 |
0 |
5 |
1.64 |
0 |
|
0.5 |
0 |
0 |
0 |
10.2 |
|
1.1 |
0 |
0 |
0 |
20.5 |
|
1.4 |
0 |
0 |
0 |
30.4 |
|
2.3 |
0 |
0 |
0 |
41.6 |
|
3.4 |
0 |
0 |
0 |
50.2 |
Of course, for each
model, you would still need a vector of 1s for the intercept, which leads to
this matrix which I call the X new matrix:
|
y1 |
x10 |
x11 |
x20 |
x21 |
x22 |
x30 |
x31 |
|
2.1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
4.5 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
|
6.8 |
1 |
3 |
0 |
0 |
0 |
0 |
0 |
|
9.4 |
1 |
4 |
0 |
0 |
0 |
0 |
0 |
|
10.8 |
1 |
5 |
0 |
0 |
0 |
0 |
0 |
|
4.8 |
0 |
0 |
1 |
1 |
0.25 |
0 |
0 |
|
9.6 |
0 |
0 |
1 |
2 |
0.42 |
0 |
0 |
|
13.7 |
0 |
0 |
1 |
3 |
0.84 |
0 |
0 |
|
19.6 |
0 |
0 |
1 |
4 |
1.32 |
0 |
0 |
|
21.4 |
0 |
0 |
1 |
5 |
1.64 |
0 |
0 |
|
0.5 |
0 |
0 |
0 |
0 |
0 |
1 |
10.2 |
|
1.1 |
0 |
0 |
0 |
0 |
0 |
1 |
20.5 |
|
1.4 |
0 |
0 |
0 |
0 |
0 |
1 |
30.4 |
|
2.3 |
0 |
0 |
0 |
0 |
0 |
1 |
41.6 |
|
3.4 |
0 |
0 |
0 |
0 |
0 |
1 |
50.2 |
In the frequentist school, the beta vector
β and the covariance matrix of the error terms ∑ are fixed
quantities. However, in the Bayesian school, β follows a normal
distribution and ∑ follows an inverse Wishart distribution.
This is the basic
way the Gibbs sampler works for the SUR model: Start off with least squares as
in the frequentist school. From that, you create the E matrix of the error
terms. Since there are 3 models and each model has 5 rows, the E matrix is a
5x3 matrix. For the above models, this would be the E matrix:
|
-0.16 |
-0.5040 |
0.1645 |
|
0.01 |
0.2414 |
0.0546 |
|
0.08 |
-0.0492 |
-0.3276 |
|
0.45 |
1.3795 |
-0.1994 |
|
-0.38 |
-1.0767 |
0.3079 |
From that, you create
the S matrix which is E’E. For the above models, this would be the S matrix:
|
0.3790 |
1.1090 |
-0.2587 |
|
1.1090 |
3.3771 |
-0.6602 |
|
-0.2587 |
-0.6602 |
0.2719 |
It should be noted
that the diagonal elements are equivalent to the sum of squared errors
(residuals) from the regression ANOVA table for each model.
To get the sigma
matrix, we divide the elements by the number of rows in each model. Since there
are 5 rows, this is the sigma matrix for the above data:
|
0.0758 |
0.2218 |
-0.0517 |
|
0.2218 |
0.6754 |
-0.1320 |
|
-0.0517 |
-0.1320 |
0.0544 |
As you notice from the above matrix, the error
terms are correlated. However, we
would like uncorrelated errors. The way we do
that is by first computing the lower Cholesky root of the sigma matrix which we
call the L matrix. This would be the result:
|
0.275318 |
0 |
0 |
|
0.805645 |
0.162314 |
0 |
|
-0.18795 |
0.119367 |
0.069388 |
We then take the
inverse of the L matrix:
|
3.6322 |
0.0000 |
0.0000 |
|
-18.0282 |
6.1609 |
0.0000 |
|
40.8517 |
-10.5985 |
14.4117 |
The dimensions of
the X new matrix are 15x7. However, the dimensions of L inverse matrix
are 3x3. To create a 15x15 matrix, we compute the Kronecker product of the L
inverse matrix and the identity matrix of dimensions 5x5, since each model has
5 rows. This is what the result looks like for the first 5 rows and columns:
|
3.6322 |
0 |
0 |
0 |
0 |
|
0 |
3.6322 |
0 |
0 |
0 |
|
0 |
0 |
3.6322 |
0 |
0 |
|
0 |
0 |
0 |
3.6322 |
0 |
|
0 |
0 |
0 |
0 |
3.6322 |
We then create the 
matrix
which is the product of the above Kronecker
product and the X new matrix.
|
14.4117 |
14.4117 |
0 |
0 |
0 |
0 |
0 |
|
3.6322 |
7.2644 |
0 |
0 |
0 |
0 |
0 |
|
3.6322 |
10.8966 |
0 |
0 |
0 |
0 |
0 |
|
3.6322 |
14.5288 |
0 |
0 |
0 |
0 |
0 |
|
3.6322 |
18.161 |
0 |
0 |
0 |
0 |
0 |
|
-18.0282 |
-18.0282 |
6.1609 |
6.1609 |
1.540225 |
0 |
0 |
|
-18.0282 |
-36.0564 |
6.1609 |
12.3218 |
2.587578 |
0 |
0 |
|
-18.0282 |
-54.0846 |
6.1609 |
18.4827 |
5.175156 |
0 |
0 |
|
-18.0282 |
-72.1128 |
6.1609 |
24.6436 |
8.132388 |
0 |
0 |
|
-18.0282 |
-90.141 |
6.1609 |
30.8045 |
10.10388 |
0 |
0 |
|
40.8517 |
40.8517 |
-10.5985 |
-10.5985 |
-2.64963 |
14.4117 |
146.9993 |
|
40.8517 |
81.7034 |
-10.5985 |
-21.197 |
-4.45137 |
14.4117 |
295.4399 |
|
40.8517 |
122.5551 |
-10.5985 |
-31.7955 |
-8.90274 |
14.4117 |
438.1157 |
|
40.8517 |
163.4068 |
-10.5985 |
-42.394 |
-13.99 |
14.4117 |
599.5267 |
|
40.8517 |
204.2585 |
-10.5985 |
-52.9925 |
-17.3815 |
14.4117 |
723.4673 |
We can also create the 
vector which
is the product of the Kronecker product and the y vector. This is what it looks
like for this data:
|
30.26457 |
|
16.3449 |
|
24.69896 |
|
34.14268 |
|
39.22776 |
|
-8.2869 |
|
-21.9823 |
|
-38.1874 |
|
-48.7114 |
|
-62.8613 |
|
42.12162 |
|
97.93992 |
|
152.7685 |
|
209.4223 |
|
263.3902 |
This is the point
at which the Bayesian approach departs from that of the frequentist school.
We start with the
prior distributions of β and ∑. To do that, we introduce some new
terms.
The 
vector is
the average of previous beta vectors. If there are no previous beta vectors, it
is a vector of 0s.
The A matrix is
known as the precision matrix. To say there is a bit of literature on this
matrix is a tad of an understatement. However, in a PDF file put together by
Peter E. Rossi (one of the authors of Bayesian Statistics and Marketing), I
found a formulation of it by multiplying the identity matrix by a scalar of
0.05. As a twist on this, I tried a scalar of the product of the number of
coefficients and 0.01. Since there are 4 X variables and 3 intercepts for a
total of 7 coefficients, the scalar for the A matrix would be 0.07.
The prior
distribution of β follows a normal distribution with the mean equal to and the
covariance matrix equal to A-1.
The V matrix is
constructed by taking the sigma matrix constructed previously and multiplying
it by the degrees of freedom v = n – k in which k represents the number of
coefficients. Since n = 15 and k = 7, we have v = 8 degrees of freedom. For
this data set, this is the V matrix:
|
0.5306 |
1.5526 |
-0.3619 |
|
1.5526 |
4.7278 |
-0.924 |
|
-0.3619 |
-0.924 |
0.3808 |
The prior
distribution of ∑ follows an inverse Wishart distribution with parameters
V and v degrees of freedom.
We now combine the
prior distributions and the data to create the posterior distributions.
In the
frequentist school, B = (X’X)-1(X’Y). However, in the Bayesian
school,
= (X’X
+ A)-1(X’Y + A).
Once is
constructed, the posterior distribution of β follows a normal distribution
with the mean of and
covariance matrix of 
.
If we assume that
the vector
is a vector of 0s, then 
.
For this data
set, this is:
|
-0.1569 |
|
2.274553 |
|
0.383083 |
|
4.328316 |
|
0.331196 |
|
-0.24892 |
|
0.066227 |
In order to generate β, we need a vector
of Z values which follows a normal distribution with mean of 0 and standard
deviation of 1. Since there are 7 coefficients, we need a vector of 7 Z values.
Suppose, the computer generates this
vector:
|
0.7839 |
|
2.5079 |
|
1.8482 |
|
-1.2640 |
|
-0.2313 |
|
-0.8057 |
|
0.2340 |
We also need the
lower Cholesky root of For
this data, the current value of this matrix is:
|
0.01062 |
-0.00452 |
0.031115 |
-0.01332 |
0.00025 |
-0.00732 |
0.000305 |
|
-0.00452 |
0.003009 |
-0.01327 |
0.008877 |
-0.00019 |
0.003126 |
-0.0002 |
|
0.031115 |
-0.01327 |
0.130568 |
-0.06583 |
0.052223 |
-0.00036 |
0.000331 |
|
-0.01332 |
0.008877 |
-0.06583 |
0.062417 |
-0.09222 |
0.003747 |
-0.00042 |
|
0.00025 |
-0.00019 |
0.052223 |
-0.09222 |
0.249939 |
-0.00112 |
4.36E-05 |
|
-0.00732 |
0.003126 |
-0.00036 |
0.003747 |
-0.00112 |
0.026158 |
-0.00078 |
|
0.000305 |
-0.0002 |
0.000331 |
-0.00042 |
4.36E-05 |
-0.00078 |
3.22E-05 |
The lower root
is:
|
0.103054 |
0 |
0 |
0 |
0 |
0 |
0 |
|
-0.04386 |
0.032934 |
0 |
0 |
0 |
0 |
0 |
|
0.301925 |
-0.00082 |
0.198514 |
0 |
0 |
0 |
0 |
|
-0.12922 |
0.097434 |
-0.13465 |
0.134514 |
0 |
0 |
0 |
|
0.002426 |
-0.00264 |
0.259367 |
-0.42169 |
0.069514 |
0 |
0 |
|
-0.07106 |
0.000278 |
0.10628 |
0.065777 |
-0.01119 |
0.073216 |
0 |
|
0.002959 |
-0.00221 |
-0.00284 |
-0.00151 |
0.00186 |
-0.00196 |
0.000919 |
Since this is a multivariate
normal distribution, we multiply the lower matrix with the Z vector and add . This is the result:
|
0.7839 |
|
2.5079 |
|
1.8482 |
|
-1.264 |
|
-0.2313 |
|
-0.8057 |
|
0.234 |
When we multiply
X and β and calculate the error terms, we can create the E matrix:
|
-1.1918 |
4.273625 |
-1.0811 |
|
-1.2997 |
10.37695 |
-2.8913 |
|
-1.5076 |
15.83809 |
-4.9079 |
|
-1.4155 |
23.11312 |
-6.6287 |
|
-2.5234 |
26.25113 |
-7.5411 |
After that, we once again create the S matrix
which is E’E:
|
13.75365 |
-141.416 |
40.85756 |
|
-141.416 |
1600.128 |
-463.527 |
|
40.85756 |
-463.527 |
134.4237 |
The posterior
distribution of ∑ follows an inverse Wishart distribution with parameters
S + V and degrees of freedom v + n in which n is the number of rows in each
model. For this data set, this is the sum of S and V:
|
14.28425 |
-139.863 |
40.49566 |
|
-139.863 |
1604.856 |
-464.451 |
|
40.49566 |
-464.451 |
134.8045 |
The degrees of
freedom are 8 + 5 = 13.
To generate ∑,
we need the T matrix. Since there are 3 models, the dimensions of the T matrix
are 3 x 3. For this data set, this is the basic setup of the T matrix:
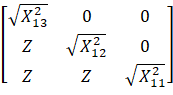
For example, 
is a
chi-square variable with 13 degrees of freedom.
Suppose, the
following T matrix is generated:
|
7.201962 |
0 |
0 |
|
-0.1135 |
15.26426 |
0 |
|
0.567206 |
0.759346 |
8.226725 |
We also need U which is the upper Cholesky
root of the S + V matrix:
|
3.779451 |
-37.0062 |
10.71469 |
|
0 |
15.34273 |
-4.42824 |
|
0 |
0 |
0.624956 |
We then generate
C = T’U:
|
51.86826 |
-2.54992 |
8.665058 |
|
0 |
232.9976 |
17.83779 |
|
0 |
0 |
67.679 |
Finally, ∑
= (C-1)(C-1)’ :
|
0.000378119 |
3.76071E-06 |
-3.72939E-05 |
|
3.76071E-06 |
1.96999E-05 |
-1.6714E-05 |
|
-3.72939E-05 |
-1.6714E-05 |
0.000218319 |
We then use this ∑ to generate
the next β and so on. After running 50,000 iterations of the Gibbs
sampler, the averages of the generated β and ∑ are calculated. This is due to the random Z and 
values that are generated in each
iteration. This is a result
for β:
|
Coefficient |
Beta
(Gibbs) |
SE
(Gibbs) |
Beta
(LS) |
SE
(LS) |
|
X10 |
0.1073 |
2.4016 |
0.03 |
0.3728 |
|
X11 |
2.2077 |
0.2182 |
2.23 |
0.1124 |
|
X20 |
1.1355 |
0.2255 |
1.1418 |
2.1708 |
|
X21 |
3.8157 |
0.0751 |
3.8261 |
2.9894 |
|
X22 |
1.3808 |
0.4142 |
1.3420 |
8.0463 |
|
X30 |
-0.3544 |
0.2041 |
-0.3674 |
0.3177 |
|
X31 |
0.0686 |
0.0002 |
0.0689 |
0.0094 |
As a comparison, the coefficients and standard errors from the individual
least square models are included. It should be noted that the standard errors
for models #2 and #3 under the Gibbs sampler are quite less than under least
squares.
After 50,000 iterations, this is a result for ∑:
|
2.187177 |
-0.62216 |
0.501253 |
|
-0.62216 |
0.188484 |
-0.13562 |
|
0.501253 |
-0.13562 |
0.183619 |
The aforementioned standard
errors are calculated by computing
In this equation, n represents the number of rows in each model, which, in
this case, is 5.
Reference:
Rossi, P.E.,
Allenby, G.M., and McCullogh, R. Bayesian
Statistics and Marketing. Chichester: John Wiley & Sons, 2005.
Zellner,
A. An Introduction to Bayesian Inference
in Econometrics. New York: John Wiley & Sons, 1970.